푼 문제는 $4k+2$+Problem 3. 근데 22번은 안풀었다. (시험범위 아님)
참고로 숙제 문제는 5,7,9,10,11,19 + Problem 3.
2. In analogy to Prop 2.5, prove that if $f$ is integrable on $\mathbb R^d$ and $\delta>0$, then
$$\lim_{\delta \to 1}\Vert f(\delta x)-f(x)\Vert_1 = 0$$
증명:
(1) $f$ 대신 Compact support continuous function $g$에 대해 증명하면 된다. 이는 다음 관찰에서 나온다:
$\mathcal C^0_c\subset L^1$는 dense하므로, $\Vert g-f\Vert_1<\epsilon$인 $g$를 찾을 수 있고, 따라서
$$\begin{align*}\Vert f(\delta x)-f(x)\Vert_1 &\leq \Vert f(\delta x)-g(\delta x)\Vert_1+\Vert g(\delta x)- g(x)\Vert_1+\Vert g(x)-f(x) \Vert_1 \\&\leq \Vert g(\delta x)-g(x)\Vert_1+(1+1/|\delta|^d)\epsilon \end{align*}$$
이다.
(2) 그러므로 그냥 $f\in \mathcal C^0_c$라고 가정하자. $f$의 support가 bounded이므로 $B_M(0)$에 속한다고 하자. 만약 $\delta$가 1에 충분히 가깝다면, $|\delta x - x|$가 임의로 작아질 수 있고 따라서 $f$의 균등연속성에 의해 $f(\delta x)-f(x)$ 역시 임의로 작아질 수 있다.
이 때 $f(\delta x)$의 support는 $B_{\delta^{-1} M}(0)$에 속하므로 $B$ $1/2<\delta$를 가정한다면 $f(\delta x)-f(x)$의 support는 $B_{2M}$에 속한다. 또한 앞선 관찰에 의해 $|f(\delta x)-f(x)|<\epsilon$이도록 하는 $\delta$를 잡을 수 있는데, 여기에 Compactness를 활용하면 이러한 $\delta$를 $x\in \overline{B_{2M}}$에서 uniform하게 잡을 수 있다. 즉 다음이 가능하다.
$$|\delta -1| << 1/2 \implies |f(\delta x)-f(x)|<\epsilon$$
그러므로, 충분히 1에 가까운 $\delta$에 대하여
$$\int_{B_{2M}}|f(\delta x)-f(x)|<v_d(2M)^d\epsilon$$
이다. 따라서 원하는 것이 보여진다. $\square$
6. $f\in L^1(\mathbb R)$ does not imply that $\lim_{x\to \infty}f(x)=0$. Show:
(a) There exists a positive continuous function $f$ on $\mathbb R$ such that $f\in L^1$ but $\limsup_{x\to \infty}f(x)=\infty$.
(b) If $f$ is uniformly continuous on $\mathbb R$ and integrable, then $\lim_{|x|\to \infty}f(x)=0$.
증명:
(a) 다음 그래프를 가지는 함수 $f$를 생각해보자.
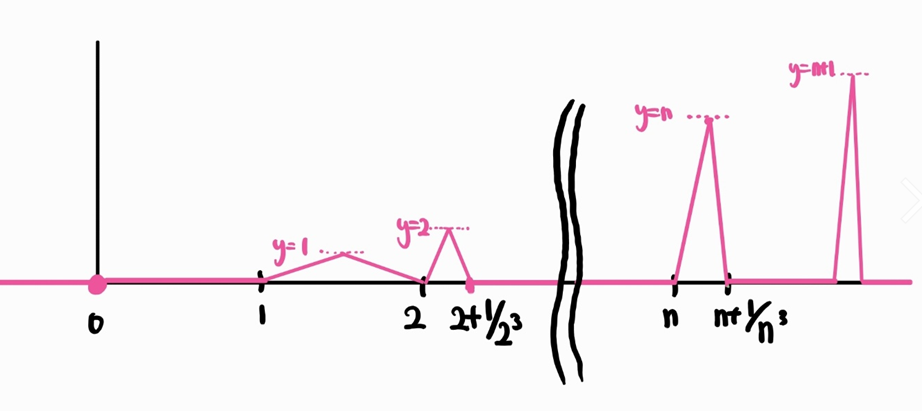
그러면
$$\begin{align*}\int |f|&=\int f\\ &=\sum^\infty\int_{[n,n+1]}f \\ &=\sum^\infty\frac{n}{2n^3}\\&<\infty\end{align*}$$
이므로 $f\in L^1$이지만, 그 무한대로의 상극한은 $\infty$이다.
(b)
만약 $\limsup_{x\to \infty}|f(x)|\neq 0$ 이면, 주어진 $\epsilon$에 대하여 증가수열 $\{x_k\}\to\infty$이 있어서
$$|f(x_k)|>2\epsilon$$
을 만족시킨다. 한편, $f$의 균등연속성을 이용하여, $$|x-y|<\delta \implies |f(x)-f(y)|<\epsilon$$이 되는 $\delta$를 찾을 수 있다.
이제 $x_{k_l}-x_{k_{l-1}}>2\delta$인 subsequence $y_l=x_{k_l}$이 존재하는데, 각 $y_l$에 대하여
$$|x-y_l|<\delta\implies |f(x)|>\epsilon$$
을 만족시키고, 각 $l$에 대하여 $[y_l-\delta,y_l+\delta]$는 disjoint하다.
그러므로 $$\int |f|\geq \sum_{l\in \mathbb N}\int_{y_l-\delta}^{y_l+\delta} |f|\geq \sum_{l\in \mathbb N}2\epsilon\delta=\infty$$
이므로, $f$가 integrable하다는 가정에 모순이다.
10. Let $f\geq 0$ and $E_{2^k}=f^{-1}(2^k,\infty)$, $F_k=f^{-1}(2^k,2^{k+1}]$. So if $f$ is finite a.e, then
$$\bigsqcup^\infty_{-\infty} F_k\overset{a.e.}{=}f^{-1}(0,\infty)$$
(문제에선 a.e.=가 아니라 그냥 =로 나와있는데 a.e.=가 맞는 것 같음)
Prove that TFAE:
- (1) $f$ is integrable
- (2) $\sum_{k\in \mathbb Z} 2^km(F_k) < \infty$
- (3) $\sum_{k\in \mathbb Z} 2^km(E_{2^k})<\infty$
Verify the following assertions:
$$f(x)=\begin{cases}|x|^{-a} & \textrm{if $|x|\leq 1$,}\\ 0 &\textrm{otherwise.}\end{cases}$$
is integrable on $\mathbb R^d$ if and only if $a<d$.
Also,
$$g(x)=\begin{cases}|x|^{-b} & \textrm{if $|x|>1$,}\\ 0 & \textrm{otherwise.}\end{cases}$$
is integrable in $\mathbb R^d$ if and only if $b>d$.
증명:
By the definition of $F_k$, $f$ is bounded between
$$\sum_{k\in \mathbb Z} 2^k\chi_{F_k}\leq f \leq \sum_{k\in \mathbb Z} 2^{k+1}\chi_{F_k}.$$
Therefore (1) iff (2).
Now observe that
$$\sum_{k\in \mathbb Z} 2^km(E_{2^k})=\sum_{k\in \mathbb Z}\sum_{n\geq k}2^km(F_n).$$
Since all the entries have nonnegative value, we can alternate the order of summation. Therefore
$$\ldots=\sum_{n\in\mathbb Z}\sum_{k\leq n} 2^km(F_n)=\sum_{n\in\mathbb Z}2^{n+1}m(F_n).$$
So we have that
$$ \sum_{k\in \mathbb Z}2^km(F_k)\leq\sum_{k\in\mathbb Z} 2^km(E_{2^k})\leq\sum_{k\in\mathbb Z}2^{k+1}m(F_k)$$
which implies (2) iff (3).
Now let's determine the integrability of $f$ and $g$ by (3).
(a가 negative일땐 쉬우므로 a가 양수인 걸 가정.)
For $f$, $$\begin{align*} & |x|^{-a}>2^k \\ \iff & \sqrt[a]{\frac{1}{2^k}}>|x|\end{align*}$$
Therefore $2^km(E_{2^k})=v_d(2^k)^{1-d/a}$. So (3) iff $a<d$.
The second one is similiar to the first one.
14. We evaluate the constant $v_d$ here. (The volume of the unit ball in $\mathbb R^d$)
(a) For $d=2$, use Corollary 3.8 to prove
$$v_2=2\int^1_{-1}(1-x^2)^{1/2}dx=\pi$$.
(b) By similar methods, show that
$$v_d=2v_{d-1}\int^1_0(1-x^2)^{(d-1)/2}dx$$.
(c) The result is
$$v_d = \frac{\pi^{d/2}}{\Gamma(d/2+1)}$$.
증명
(a) Remark. Lemma 3.8 states that ''the volume below the graph'' is equal to ''the integral of the function''. So, this is immediate.
(b) See below.
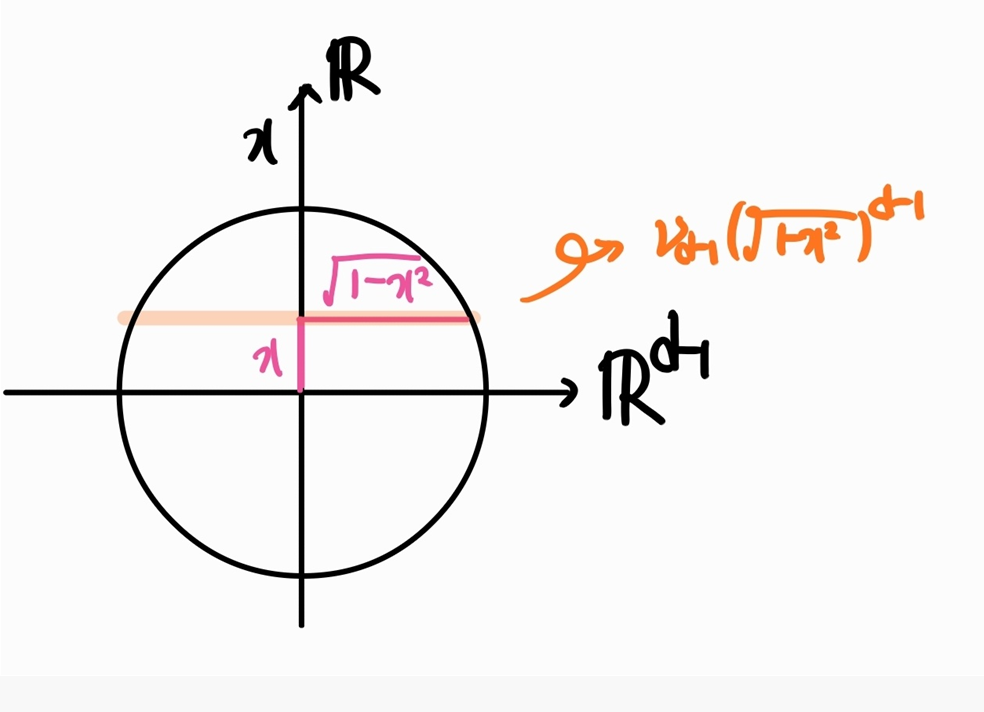
(c) Substitute $x$ into $\cos \theta$, we have
$$\begin{align*}&\int_0^1\sqrt{1-x^2}^{d-1}dx\\&=\int_{3/2\pi}^{2\pi}-|\sin^{d-1}\theta|\sin{\theta} d\theta \\&=\int_0^{\pi/2}\sin^d{\theta}d\theta \\& =\begin{cases}\frac{(d-1)!!}{d!!}\cdot\frac{\pi}{2}&\textrm{$d$ is even}\\ \frac{(d-1)!!}{d!!} &\textrm{$d$ is odd}\end{cases}\end{align*}$$
Therefore, by (b),
$$\begin{align*}v_d&=2^d\prod_{i=1}^d\int_0^1 f_i(x)dx \\&=2^d\left(\frac{0!!}{1!!}\cdots \frac{(d-2)!!}{(d-1)!!}\cdot\frac{(d-1)!!}{d!!}\right) \left(\frac{\pi}{2}\right)^{\lfloor d/2 \rfloor} \\& = \frac{2^d}{d!!}\left(\frac{\pi}{2}\right)^{\lfloor d/2\rfloor} \\& = \frac{\pi^{d/2}}{\Gamma(d/2+1)},\end{align*}$$
considering $\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}$ and the parity of $d$.
18. Let $f$ be a measurable finite-valued function on $[0,1]$, and suppose that $|f(x)-f(y)|$ is integrable on $[0,1]\times [0,1]$. Show that $f$ is integrable on $[0,1]$.
증명
푸비니 정리에 의해, 고정된 상수 $y_0\in [0,1]$가 있어서 $|f(x)-f(y_0)|$가 $[0,1]$ 위에서 르벡적분 가능하다. (cf. 사실 이런 $y_0$는 a.e. in $[0,1]$.)
따라서, 다음이 성립하며 $f$는 $[0,1]$ 위에서 적분가능하다.
$$\int_{[0,1]} |f(x)|dx\leq \int_{[0,1]}|f(x)-f(y_0)|+|f(y_0)|dx<\infty$$
Problem 3.
A sequence $\{f_k\}$ of m'ble functions on $\mathbb R^d$ is Cauchy in sequence if for every $\epsilon>0$,
$$m(\{x:|f_k(x)-f_l(x)|>\epsilon\})\to 0\textrm{ as $k,l\to \infty$. }$$
A sequence$\{f_k\}$ of m'ble functions on $\mathbb R^d$ is Converges in measure to a function $f$ if for every $\epsilon>0$,
$$m(\{x:|f_k(x)-f(x)|>\epsilon\})\to 0\textrm{ as $k\to \infty$. }$$
Prove that for a sequence of integrable functions $\{f_k\}$,
$$f_k \overset{L^1}{\longrightarrow} f \implies f_k \overset{\textrm{measure}}{\longrightarrow} f$$.
Is the converse true?
증명
Cauchy in sequence는 그냥 소개해준 것 같고.. (문제랑 아무 상관 없고) 귀류법을 써서 증명하기 위해 Converge in measure를 논리기호로 써보면
$$^\forall \epsilon>0, ^\forall \delta>0, ^\exists K :\;^\forall k>K,\;m(\{x:|f_k(x)-f(x)|>\epsilon\})<\delta $$
이고 이걸 부정하면
$$^\exists \epsilon_0>0, ^\exists \delta_0>0, ^{\exists\infty}k>0: \;m(\{x:|f_k(x)-f(x)|>\epsilon_0\})\geq \delta_0$$
이다. 저기서 $f_k$의 부분수열을 그냥 WLOG 전체 수열이라고 가정하자. $E_k:=\{x:|f_k(x)-f(x)|>\epsilon_0\}$라 하면,
$$\int |f_k-f|\geq \int_{E_{k}}|f_{k}-f|\geq \delta_0\epsilon_0$$
이므로 $\Vert f_k-f \Vert_1$은 $0$으로 수렴할 수 없다.
반대로, 역의 반례를 들어보도록 해보자. 다음 함수
$$f_k=k^2\chi_{[0,1/k]}$$
의 경우, $f_k$는 $0$으로 측도 상 수렴하지만 $L_1$ 상 수렴하지 않는다.
김 모 양의 입시일정으로 7번 문제를 따로 풀게 되었다.
7. Let $\Gamma\subset \mathbb R^d \times \mathbb R$ be a graph of a measurable function $f: \mathbb R^d\to \mathbb R$. Show that $\Gamma$ is a measurable subset of $\mathbb R^{d+1}$ with measure $0$.
증명.
다음을 보이면 Countable Additivity를 이용해서 문제가 증명되므로, 다음은 이 문제의 충분조건이다.
The graph of $f:[0,1]^d\to \mathbb R$ has measure $0$.
이 명제는 다음을 통해 보여진다.
$\Gamma= \bigcup_{n\in \mathbb Z}\left(\Gamma\cap\left([0,1]^d\times [n\epsilon,(n+1)\epsilon)\right)\right)$
이때 $\Gamma\cap [n\epsilon,(n+1)\epsilon)$을 $(0,\cdots,0,-n)$으로 translate 해서 마지막 좌표가 $[0,\epsilon)$에 속하도록 할 수 있다. 이를 $\Gamma_n$이라 하자. 그러면, $\Gamma_n$은 모두 disjoint하다. (함수의 성질)
따라서,
$$\begin{align*} m(\Gamma)&=m\left(\bigsqcup_{n\in\mathbb Z} \Gamma\cap ([0,1]^d\times[n\epsilon, (n+1)\epsilon))\right) \\& = \sum _{n\in \mathbb Z} m(\Gamma\cap \left([0,1]^d\times[n\epsilon, (n+1)\epsilon)\right)) \\& = \sum_n m(\Gamma_n)\\& =m(\bigsqcup \Gamma_n)\\&\leq m([0,1]^d\times[0,\epsilon))\\& =\epsilon\end{align*}$$
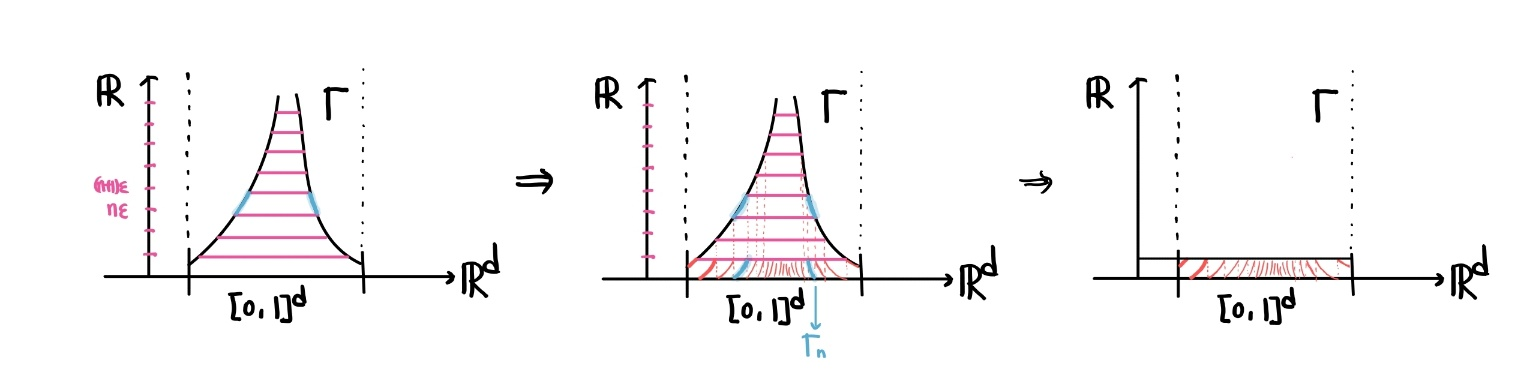
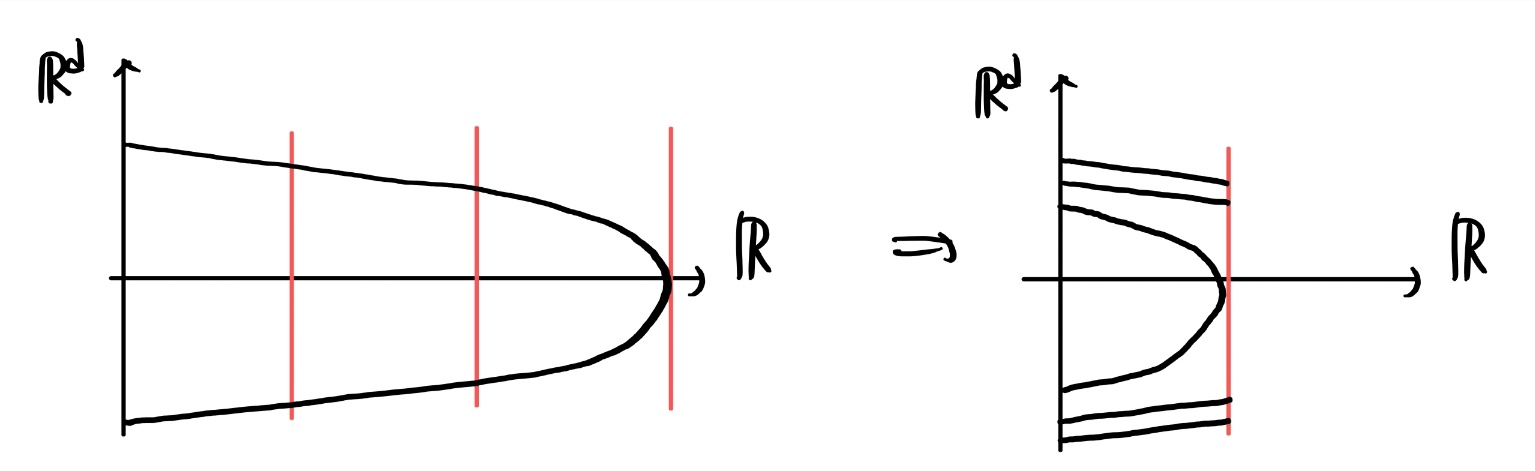
함수 그래프를 변형시키는게 마치 삼단봉을 집어넣는 것 같다고 이야기 했더니 몰매를 맞을 뻔 했다.

'기타 > 시험 관련' 카테고리의 다른 글
| Stein 3장 연습문제 (0) | 2024.04.29 |
|---|---|
| 대수학1 중간고사 대비 (0) | 2024.04.24 |
| 미다체 중간고사 복기 (0) | 2024.04.22 |
| 해석학1 중간고사1 복기 (0) | 2024.04.21 |