Stein 2장 연습문제

푼 문제는 $4k+2$+Problem 3. 근데 22번은 안풀었다. (시험범위 아님)

참고로 숙제 문제는 5,7,9,10,11,19 + Problem 3.

 

2. In analogy to Prop 2.5, prove that if $f$ is integrable on ${\mathbb{R}}^d$ and $\delta >0$, then 

$$\underset{\delta \to 1}{lim}\Vert f(\delta x)-f(x){\Vert }_1=0$$

증명:

(1) $f$ 대신 Compact support continuous function $g$에 대해 증명하면 된다. 이는 다음 관찰에서 나온다:

${\mathcal{C}}_c^0\subset L^1$는 dense하므로, $\Vert g-f{\Vert }_1<ϵ$인 $g$를 찾을 수 있고, 따라서

 

$$\begin{array}{rl}\Vert f(\delta x)-f(x){\Vert }_1& \le \Vert f(\delta x)-g(\delta x){\Vert }_1+\Vert g(\delta x)-g(x){\Vert }_1+\Vert g(x)-f(x){\Vert }_1\\ & \le \Vert g(\delta x)-g(x){\Vert }_1+(1+1/|\delta {|}^d)ϵ\end{array}$$

 

이다.

 

(2) 그러므로 그냥 $f\in {\mathcal{C}}_c^0$라고 가정하자. $f$의 support가 bounded이므로 $B_M(0)$에 속한다고 하자. 만약 $\delta$가 1에 충분히 가깝다면, $|\delta x-x|$가 임의로 작아질 수 있고 따라서 $f$의 균등연속성에 의해 $f(\delta x)-f(x)$ 역시 임의로 작아질 수 있다.

이 때 $f(\delta x)$의 support는 $B_{{\delta }^{-1}M}(0)$에 속하므로 $B$ $1/2<\delta$를 가정한다면 $f(\delta x)-f(x)$의 support는 $B_{2M}$에 속한다. 또한 앞선 관찰에 의해 $|f(\delta x)-f(x)|<ϵ$이도록 하는 $\delta$를 잡을 수 있는데, 여기에 Compactness를 활용하면 이러한 $\delta$를 $x\in \overline{B_{2M}}$에서 uniform하게 잡을 수 있다. 즉 다음이 가능하다.

$$|\delta -1|<<1/2⟹|f(\delta x)-f(x)|<ϵ$$

 

그러므로, 충분히 1에 가까운 $\delta$에 대하여 

$${\int }_{B_{2M}}|f(\delta x)-f(x)|<v_d(2M{)}^dϵ$$

이다. 따라서 원하는 것이 보여진다. $◻$

---

6. $f\in L^1(\mathbb{R})$ does not imply that $\underset{x\to \mathrm{\infty }}{lim}f(x)=0$. Show:

(a) There exists a positive continuous function $f$ on $\mathbb{R}$ such that $f\in L^1$ but $\underset{x\to \mathrm{\infty }}{lim sup}f(x)=\mathrm{\infty }$.

(b) If $f$ is uniformly continuous on $\mathbb{R}$ and integrable, then $\underset{|x|\to \mathrm{\infty }}{lim}f(x)=0$.

증명:

(a) 다음 그래프를 가지는 함수 $f$를 생각해보자. 

그러면

$$\begin{array}{rl}\int |f|& =\int f\\ & =\sum ^{\mathrm{\infty }}{\int }_{[n,n+1]}f\\ & =\sum ^{\mathrm{\infty }}\frac{n}{2n^3}\\ & <\mathrm{\infty }\end{array}$$

이므로 $f\in L^1$이지만, 그 무한대로의 상극한은 $\mathrm{\infty }$이다.

 

(b)

만약 $\underset{x\to \mathrm{\infty }}{lim sup}|f(x)|\ne 0$ 이면, 주어진 $ϵ$에 대하여 증가수열 $\{x_k\}\to \mathrm{\infty }$이 있어서

$$|f(x_k)|>2ϵ$$

을 만족시킨다. 한편, $f$의 균등연속성을 이용하여, $$|x-y|<\delta ⟹|f(x)-f(y)|<ϵ$$이 되는 $\delta$를 찾을 수 있다.

이제 $x_{k_l}-x_{k_{l-1}}>2\delta$인 subsequence $y_l=x_{k_l}$이 존재하는데, 각 $y_l$에 대하여

$$|x-y_l|<\delta ⟹|f(x)|>ϵ$$

을 만족시키고, 각 $l$에 대하여 $[y_l-\delta ,y_l+\delta ]$는 disjoint하다.

 

그러므로 $$\int |f|\ge \sum _{l\in \mathbb{N}}{\int }_{y_l-\delta }^{y_l+\delta }|f|\ge \sum _{l\in \mathbb{N}}2ϵ\delta =\mathrm{\infty }$$

이므로, $f$가 integrable하다는 가정에 모순이다.

---

10. Let $f\ge 0$ and $E_{2^k}=f^{-1}(2^k,\mathrm{\infty })$, $F_k=f^{-1}(2^k,2^{k+1}]$. So if $f$ is finite a.e, then 

$$\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{⨆}}{F}_k\stackrel{a.e.}{=}{f}^{-1}(0,\mathrm{\infty })$$

(문제에선 a.e.=가 아니라 그냥 =로 나와있는데 a.e.=가 맞는 것 같음)

 

Prove that TFAE:

• (1) $f$ is integrable
• (2) $\sum _{k\in \mathbb{Z}}{2}^{k}m(F_k)<\mathrm{\infty }$
• (3) $\sum _{k\in \mathbb{Z}}{2}^{k}m(E_{2^k})<\mathrm{\infty }$

Verify the following assertions:

$$f(x)=\{\begin{array}{ll}|x{|}^{-a}& \text{if }|x|\le 1\text{,}\\ 0& \text{otherwise.}\end{array}$$

is integrable on ${\mathbb{R}}^d$ if and only if $a<d$.

Also,

$$g(x)=\{\begin{array}{ll}|x{|}^{-b}& \text{if }|x|>1\text{,}\\ 0& \text{otherwise.}\end{array}$$

is integrable in ${\mathbb{R}}^d$ if and only if $b>d$. 

증명:

By the definition of $F_k$,  $f$ is bounded between

 

$$\sum _{k\in \mathbb{Z}}{2}^k{\chi }_{F_k}\le f\le \sum _{k\in \mathbb{Z}}{2}^{k+1}{\chi }_{F_k}.$$

 

Therefore (1) iff (2).

 

Now observe that

 

$$\sum _{k\in \mathbb{Z}}{2}^{k}m(E_{2^k})=\sum _{k\in \mathbb{Z}}\sum _{n\ge k}{2}^{k}m(F_n).$$

 

Since all the entries have nonnegative value, we can alternate the order of summation. Therefore

 

$$\dots =\sum _{n\in \mathbb{Z}}\sum _{k\le n}{2}^{k}m(F_n)=\sum _{n\in \mathbb{Z}}{2}^{n+1}m(F_n).$$ 

 

So we have that

 

$$\sum _{k\in \mathbb{Z}}{2}^{k}m(F_k)\le \sum _{k\in \mathbb{Z}}{2}^{k}m(E_{2^k})\le \sum _{k\in \mathbb{Z}}{2}^{k+1}m(F_k)$$

 

which implies (2) iff (3).

 

Now let's determine the integrability of $f$ and $g$ by (3).

(a가 negative일땐 쉬우므로 a가 양수인 걸 가정.)

For $f$, $$\begin{array}{rl}& |x{|}^{-a}>2^k\\ ⟺& \sqrt[a]{\frac{1}{2^k}}>|x|\end{array}$$

 

Therefore $2^{k}m(E_{2^k})=v_d(2^k{)}^{1-d/a}$. So (3) iff $a<d$.

 

The second one is similiar to the first one.

 

---

14. We evaluate the constant $v_d$ here. (The volume of the unit ball in ${\mathbb{R}}^d$)

 

(a) For $d=2$, use Corollary 3.8 to prove

$$v_2=2{\int }_{-1}^1(1-x^2{)}^{1/2}dx=\pi$$.

 

(b) By similar methods, show that 

$$v_d=2v_{d-1}{\int }_0^1(1-x^2{)}^{(d-1)/2}dx$$.

 

(c) The result is 

$$v_d=\frac{{\pi }^{d/2}}{\mathrm{\Gamma }(d/2+1)}$$.

 

증명

(a) Remark. Lemma 3.8 states that ''the volume below the graph'' is equal to ''the integral of the function''. So, this is immediate.

 

(b) See below.

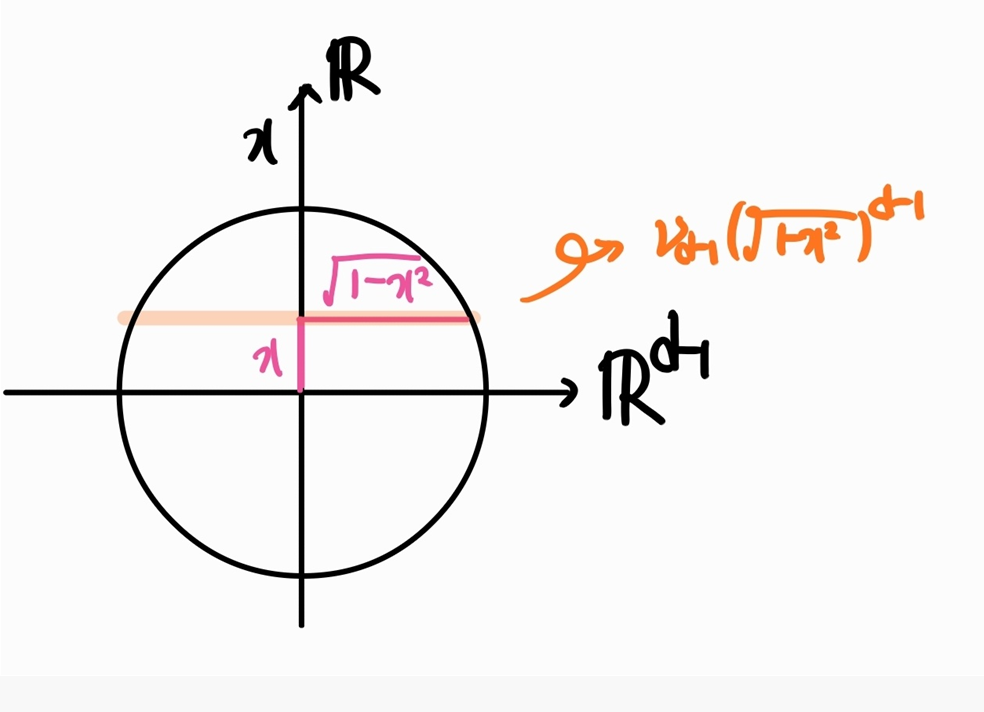
(c) Substitute $x$ into $\cos \theta$, we have

 

$$\begin{array}{rl}& {\int }_0^1{\sqrt{1-x^2}}^{d-1}dx\\ & ={\int }_{3/2\pi }^{2\pi }-|{\sin }^{d-1}\theta |\sin \theta d\theta \\ & ={\int }_0^{\pi /2}{\sin }^d\theta d\theta \\ & =\{\begin{array}{ll}\frac{(d-1)!!}{d!!}\cdot \frac{\pi }{2}& d\text{ is even}\\ \frac{(d-1)!!}{d!!}& d\text{ is odd}\end{array}\end{array}$$

 

Therefore, by (b),

$$\begin{array}{rl}{v}_d& =2^d\prod _{i=1}^d{\int }_0^1{f}_i(x)dx\\ & =2^d(\frac{0!!}{1!!}\cdots \frac{(d-2)!!}{(d-1)!!}\cdot \frac{(d-1)!!}{d!!}){\left(\frac{\pi }{2}\right)}^{\lfloor d/2\rfloor }\\ & =\frac{2^d}{d!!}{\left(\frac{\pi }{2}\right)}^{\lfloor d/2\rfloor }\\ & =\frac{{\pi }^{d/2}}{\mathrm{\Gamma }(d/2+1)},\end{array}$$

 

considering $\mathrm{\Gamma }\left(\frac{1}{2}\right)=\sqrt{\pi }$ and the parity of $d$.

---

18. Let $f$ be a measurable finite-valued function on $[0,1]$, and suppose that $|f(x)-f(y)|$ is integrable on $[0,1]\times [0,1]$. Show that $f$ is integrable on $[0,1]$.

 

증명

푸비니 정리에 의해, 고정된 상수 $y_0\in [0,1]$가 있어서 $|f(x)-f(y_0)|$가 $[0,1]$ 위에서 르벡적분 가능하다. (cf. 사실 이런 $y_0$는 a.e. in $[0,1]$.)

따라서, 다음이 성립하며 $f$는 $[0,1]$ 위에서 적분가능하다.

$${\int }_{[0,1]}|f(x)|dx\le {\int }_{[0,1]}|f(x)-f(y_0)|+|f(y_0)|dx<\mathrm{\infty }$$

---

Problem 3.

A sequence $\{f_k\}$ of m'ble functions on ${\mathbb{R}}^d$ is Cauchy in sequence if for every $ϵ>0$,

$$m(\{x:|f_k(x)-f_l(x)|>ϵ\})\to 0\text{ as }k,l\to \mathrm{\infty }\text{. }$$

 

A sequence$\{f_k\}$ of m'ble functions on ${\mathbb{R}}^d$ is Converges in measure to a function $f$ if for every $ϵ>0$,

$$m(\{x:|f_k(x)-f(x)|>ϵ\})\to 0\text{ as }k\to \mathrm{\infty }\text{. }$$

 

Prove that for a sequence of integrable functions $\{f_k\}$,

$$f_k\stackrel{L^1}{⟶}f⟹f_k\stackrel{\text{measure}}{⟶}f$$.

 

Is the converse true?

 

증명

Cauchy in sequence는 그냥 소개해준 것 같고.. (문제랑 아무 상관 없고) 귀류법을 써서 증명하기 위해 Converge in measure를 논리기호로 써보면

 

$${}^{\mathrm{\forall }}ϵ>0{,}^{\mathrm{\forall }}\delta >0{,}^{\mathrm{\exists }}K:{}^{\mathrm{\forall }}k>K,m(\{x:|f_k(x)-f(x)|>ϵ\})<\delta$$

 

이고 이걸 부정하면

 

$${}^{\mathrm{\exists }}{ϵ}_0>0{,}^{\mathrm{\exists }}{\delta }_0>0{,}^{\mathrm{\exists }\mathrm{\infty }}k>0:m(\{x:|f_k(x)-f(x)|>{ϵ}_0\})\ge {\delta }_0$$

 

이다. 저기서 $f_k$의 부분수열을 그냥 WLOG 전체 수열이라고 가정하자. $E_k:=\{x:|f_k(x)-f(x)|>{ϵ}_0\}$라 하면,

 

$$\int |f_k-f|\ge {\int }_{E_k}|f_k-f|\ge {\delta }_0{ϵ}_0$$

 

이므로 $\Vert f_k-f{\Vert }_1$은 $0$으로 수렴할 수 없다.

 

반대로, 역의 반례를 들어보도록 해보자. 다음 함수

$$f_k=k^2{\chi }_{[0,1/k]}$$

의 경우, $f_k$는 $0$으로 측도 상 수렴하지만 $L_1$ 상 수렴하지 않는다. 

 

 

---

 

김 모 양의 입시일정으로 7번 문제를 따로 풀게 되었다.

 

7. Let $\mathrm{\Gamma }\subset {\mathbb{R}}^d\times \mathbb{R}$ be a graph of a measurable function $f:{\mathbb{R}}^d\to \mathbb{R}$. Show that $\mathrm{\Gamma }$ is a measurable subset of ${\mathbb{R}}^{d+1}$ with measure $0$.

 

증명.

다음을 보이면 Countable Additivity를 이용해서 문제가 증명되므로, 다음은 이 문제의 충분조건이다.

 

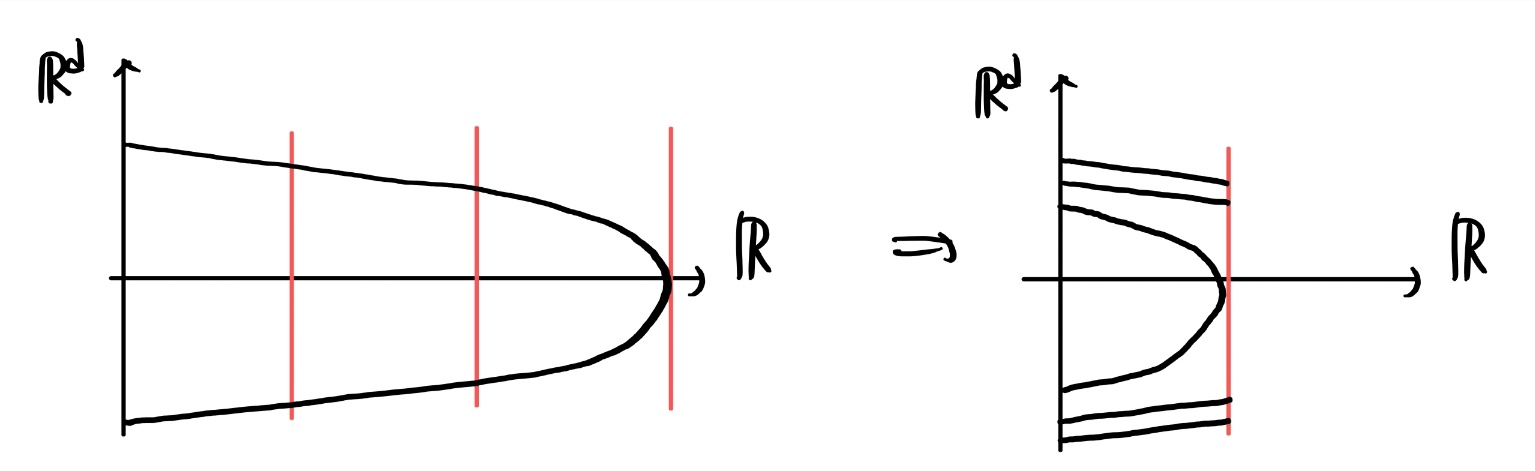
The graph of $f:[0,1{]}^d\to \mathbb{R}$ has measure $0$.

 

이 명제는 다음을 통해 보여진다.

 

$\mathrm{\Gamma }=\bigcup _{n\in \mathbb{Z}}(\mathrm{\Gamma }\cap ([0,1{]}^d\times [nϵ,(n+1)ϵ)))$

이때 $\mathrm{\Gamma }\cap [nϵ,(n+1)ϵ)$을 $(0,\cdots ,0,-n)$으로 translate 해서 마지막 좌표가 $[0,ϵ)$에 속하도록 할 수 있다. 이를 ${\mathrm{\Gamma }}_n$이라 하자. 그러면, ${\mathrm{\Gamma }}_n$은 모두 disjoint하다. (함수의 성질)

 

따라서, 

$$\begin{array}{rl}m(\mathrm{\Gamma })& =m(\underset{n\in \mathbb{Z}}{⨆}\mathrm{\Gamma }\cap ([0,1{]}^d\times [nϵ,(n+1)ϵ)))\\ & =\sum _{n\in \mathbb{Z}}m(\mathrm{\Gamma }\cap ([0,1{]}^d\times [nϵ,(n+1)ϵ)))\\ & =\sum _{n}m({\mathrm{\Gamma }}_n)\\ & =m(⨆{\mathrm{\Gamma }}_n)\\ & \le m([0,1{]}^d\times [0,ϵ))\\ & =ϵ\end{array}$$

 

 

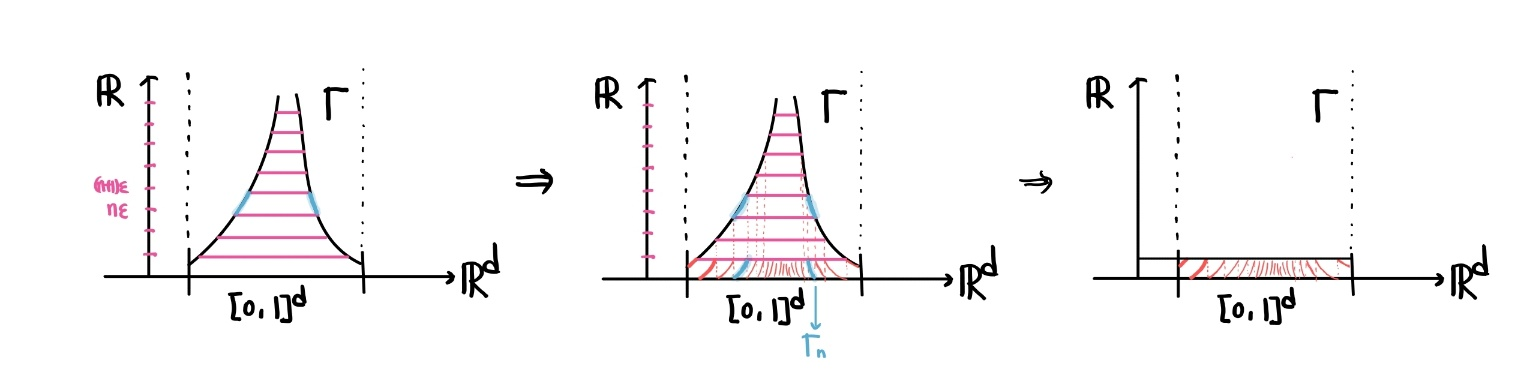
함수 그래프를 변형시키는게 마치 삼단봉을 집어넣는 것 같다고 이야기 했더니 몰매를 맞을 뻔 했다.

삼단봉. 위병소 근무의 추억.

삼단봉(?)